Math and Physics’ Divorce, Poetry, and the Scientific Slowdown
An alternative hypothesis to the 'burden of knowledge' theory of the slowdown
From a historical perspective, the burden of knowledge hypothesis is flimsy. For those who don’t know, I’m referring to the hypothesis that scientific ideas get significantly more difficult to find as knowledge continually progresses. My lack of faith in the hypothesis does not stem from some knee-jerk reaction against hypotheses that imply human progress will slow down. In fact, I used to assume that the burden of knowledge hypothesis was true.
But as I’ve continued to explore the history of early-to-mid 1900s science — which largely occurred in a period pre-dating the best micro-level data we see in the economics of innovation literature — I’ve become much more skeptical.
I’m not saying that as more and more things are known in a field, it doesn’t take longer to learn each of them. That is, of course, true. It takes longer to learn more things than it does fewer things. But what I am saying is that the accumulation of additional knowledge as the primary driver of our slowing rate of scientific progress is flimsy as a hypothesis. There are other theories that can fit the trends in the data just as well; one of these theories was put forward by scientists living through the mid-1900s who felt they were observing the onset of new branches of science becoming harder and harder to create.
Accounts I’ve come across of WW2-era physicists complaining about academia becoming a worse place to do creative or interdisciplinary work do not point to the growing size of the literature as the reason. Interestingly, their complaints had nothing to do with the growing size of hypothetical ‘idea space’ at all; their complaints often blamed administrative changes. They point to things like growing conference sizes or scientific meetings being held for narrower and narrower sub-branches of work rather than broad areas — human organization problems.
Today’s piece will put forward an alternative hypothesis as the primary driver of the scientific slowdown: the human systems hypothesis.
To inform different aspects of the hypothesis, I’ll examine:
What the existing evidence from the economics literature does and does not say about the burden of knowledge
Why many great mid-1900s scientists blamed human organization problems for the growing difficulty in asking new, big questions
Why the exact nature of math and physics’ ‘divorce’ supports the human systems hypothesis
And how the field of poetry — whose rate of progress is likely not vulnerable to burden of knowledge issues — suffered a similar fate to that of science when institutions like those in late-1900s science were introduced
Let’s get into it.

For those who listened to the Edison podcast, please feel free to comment or DM me topics that you’d like to see covered on the podcast!
For the sake of this piece, ‘interdisciplinary work’ should be defined as work that draws from and/or is relevant to multiple disciplines.
This piece, as always, is done in concert with the Good Science Project
I should state upfront that I don’t expect this hypothesis to win over a majority of the economists. The reason is that there is not exactly a single, clean ‘identification strategy’ to verify the theory. Most imaginable ‘natural experiments’ in the modern context would not approach any kind of clean answer. An unwieldy number of changes occurred in the culture, organization, and incentives of science that affected an entire generation of researchers and have continued to affect each generation afterward. Any single accidental change to one component would still leave most others intact.
So, instead, I employ a style of argument more familiar to later-1900s political science literature in which I attempt to fold in all available data into the theory, but am very willing to let relevant qualitative information inform pieces of the hypothesis when it makes sense to do so. This style of work was often used in areas such as later-1900s comparative economic development work. In a case like this, they had before them:
A very specific and biased set of countries that had achieved 'developed country' status
Some high-level data on most countries
Some more granular data on some — mostly developed ones
Detailed qualitative histories from many countries going back centuries
But no data that was nearly specific enough or numerous enough to begin answering the question in a purely quantitative way
But the stakes were large and the questions were worth answering as best they could, so those studying economic development tried and used all the information at their disposal. For those readers familiar with the subject, works by people like Mancur Olson exemplify this tradition and are examples of this style done at the highest level.
With that explanation out of the way, let’s explore the argument.
A brief overview of the existing economics of innovation evidence
To start, I should briefly go over what has been confirmed by data in the existing economics of innovation literature and what has not on the question of the burden of knowledge.
Are ideas getting harder to find?
Whether ideas are getting harder to find or not is very much an open question — or at least has some notable caveats. What researchers like Bloom et al. have confirmed is that our research productivity across the board very likely seems to have been decreasing since about 1970 — give or take. As we’ve spent more money and more researchers than ever have poured into fields, we are getting less and less productive.
The following graphics from Bloom et al.’s famous paper demonstrates this disappointing trend on the micro-level, within fields. Some of the y-axes variables are more convincing than others — i.e. many would believe that transistor count is more robust than counting the number of clinical trials — but the general trends the paper observes seem quite robust and clear: we’ve been getting steadily less impressive outcomes compared to what we’ve been putting in since about 1970.
Now, all of this micro-level data only goes back to around 1970-ish — a little before in a few cases. A portion of the introduction of their paper paper — which introduces the topic using very macro, national trends — goes back as early as 1930. However, many question the ability of economy-wide metrics like TFP growth on one axis and total US expenditure in R&D on the other to be useful in understanding these questions since the metrics capture so many other trends that one can’t control for — particularly in a mid-1900s American science landscape where how research was used and invested in was rapidly transforming. The authors were aware of this, which is why they dove into the micro-level data shown above. The result was a fantastic and robust paper identifying a massive problem in American science from about 1970 onward.
As those micro-level charts show, in almost all research areas explored in the literature, we seem to be getting as little research productivity per dollar as ever. Of course, these fields do not cover everything. But they were selected because they were generally measurable. And I think that approach makes a lot of sense. From those graphs, it seems very likely that we’re not as productive as we used to be. That is hard to argue with — I wouldn’t argue it.
The natural next question is, “Is this our fault?”
Are ideas getting harder to find by some almost natural force? Or have we gotten worse at doing science somehow?
The ‘natural force’ supporters often believe that ideas just get harder to find because previous generations have somehow picked all the lower-hanging fruit. This implies that the lack of research productivity is not humanity’s fault, it’s just that we’re increasingly fighting an uphill battle.
Does the economics of innovation literature disentangle this question at all?
The Burden of Knowledge and the ‘Death of the Renaissance Man’
In short, not exactly.
When you trace ‘burden of knowledge’ up the citation tree in the economics literature, all roads lead you to Ben Jones at Northwestern. His big initial paper on the topic, for which this section is named, and a later paper called Age dynamics in scientific creativity confirm some things about the burden of knowledge, to be sure, but they don’t do anything to pin down the burden of knowledge as the primary factor in the slowdown of scientific ideas.
The first paper is not causal. It is a structural modeling paper with a portion dedicated to the analysis of some patent data from a high level. The paper, in a nutshell, posits what a good model of burden of knowledge-like dynamics would be if the dynamics existed. The data don’t confirm strong causality, simply that the theory put forward more or less can mesh with a reality in which the trends in the data exist. The data that the author used to fit his theory to was basic patent data noting things like team size and age of invention.
Even with this basic data, the theory hardly fit cleanly. The biggest reason I say this is that, even though he acknowledged some patent areas were more complex than others, he noted that:
Innovators in the same cohort choose the same amount of education across different areas of application. What is particularly surprising is that this result holds even though some areas may feature a greater difficulty in reaching the frontier of knowledge.
He attempts to fit this observation into the theory with a hypothetical explanation of how innovators could allocate themselves in a way that could make this consistent with the theory.
You get the idea. The paper surely empirically shows certain relationships — and I do genuinely love the paper — but it’s far from a ‘nail in the coffin’ for competing theories.
However, Jones did extend the idea further. He, along with Bruce Weinberg, wrote a fascinating follow-up paper using all of the physics, chemistry, and medicine Nobel Prize-winning discoveries from 1900-2008 as their dataset. Some relevant trends the authors observe are:
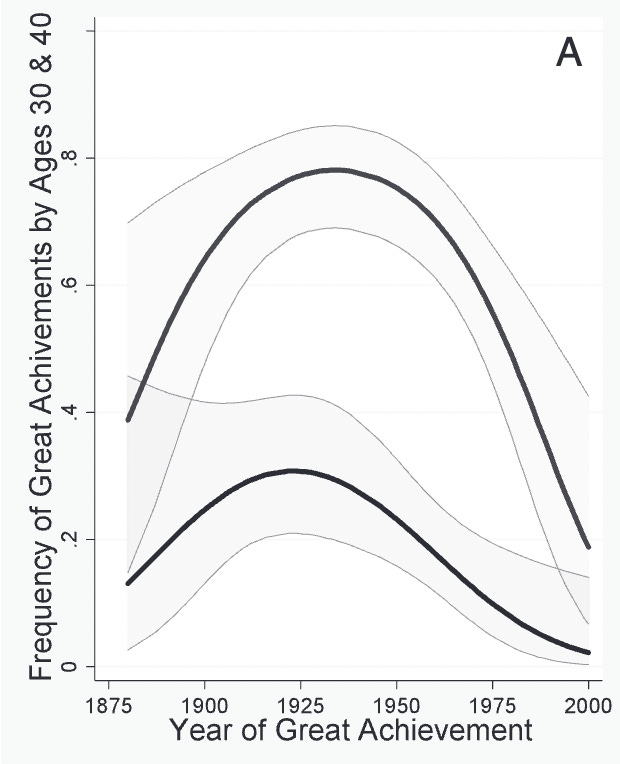
The proportion of Nobel-winners who make their Nobel-winning discovery by the age of 30 or 40 is going down drastically.
Theoretical contributions are associated with younger researchers.
Physics Nobel winners showed a substantial burst in youthful productivity after quantum mechanics burst onto the scene in their field.
The following graph displays this youth boom in physics. The lower line is the percentage of Nobels given out to researchers who made their winning discovery by the age of 30, and the upper line by the age of 40. The quantum era seems to have initiated a steadily rising level of outstanding discoveries from young researchers, peaking in the 1930s.
I’ll re-examine more specific evidence from this paper later in the piece — once I’ve further fleshed out the historical argument for the human systems hypothesis. For now, I’d like to bring attention to a key caveat that the authors noted in explaining how this new branch of physics affected the trend of Nobel-prize winners getting increasingly older:
Age dynamics might be associated with changes in a field’s foundational knowledge, which may typically expand with time but also may contract in cases where new knowledge devalues old knowledge. Heisenberg [who won his Nobel for work done at 23 and 25], for example, nearly failed his PhD examinations at age 21, because he knew little of classical electromagnetism; his contributions in the subsequent 4 years suggest that training in classical physics may have become less salient.
This is a fantastic observation from the authors and one that often gets lost in discussions of the burden of knowledge. The concept of the burden of knowledge and its relationship with scientific productivity is one that cannot be disentangled from the concept of scientific branch-creation. The older the branch, the more the 'burdensome' of the burden of knowledge is; the younger the branch, the more negligible it becomes.
This observation, along with the oddity that fields of varying complexity have similar training times in Jones’ first paper, will fit very cleanly into the human systems hypothesis.
The historical perspective leads one to the human systems hypothesis
The reasons fields seem to grow apart, when one reads the historical sources, are quite interesting. The growing apart process often seems much more abrupt than the rate of change in the scientific fields themselves.
The opinions of many of the researchers themselves are the first point that lead me to this observation. The growing apart of fields in the years leading up to 1970 did not go unnoticed by researchers at the time. Researchers who lived through great eras of their fields in the early-1900s and continued to research through the 1970s point the finger at things like conference sizes and not the size of the literature as responsible for it becoming harder to do truly exploratory research. This group is interesting because many of them started out in fields that were smaller but explosively growing in terms of ideas and continued to research into the era in which the number of publications exploded but the rate of big ideas in their fields did not seem to be exploding.
To be clear, the growth in the size of the literature was surely noticed…
It’s material that great minds who thought critically about their fields chose not to complain about this growth in the size of the literature as much as things like conference sizes and incentives. Just because the early-1900s was an era in which one could try to keep up with all the literature in related fields just by reading it, that doesn't mean that's what researchers usually did. The accounts in this section paint a picture of researchers who largely kept up with science by keeping up with people.
The second point that leads me to this observation relates to the importance of how fields grow apart. The exact nature of how fields come together and grow apart often has more to do with people and incentives than ideas themselves. A supporter of the burden of knowledge hypothesis would likely expect that fields that were formerly very interrelated would grow apart somewhat gradually as keeping all the ideas in one's head became more and more untenable. Fields separating, usually, should not be for some interpersonal reason or internal politics. But this abrupt separation is often exactly what one finds.
I’ll use the accounts of mid-1900s physicists to explore both of these points.
Mid-1900s physicists point the finger at systems changes
Many World War II-era physicists were not only practicing researchers in the small and bustling field of early-1900s physics, but continued on as researchers well into the 1970s. As there was an explosion of publications in their field, the researcher accounts I’ve come across do contain complaints from the old-guard researchers. Several prominent examples note the feeling that academia was increasingly becoming a worse place to do creative or interdisciplinary work, but the complaints don’t pertain to the number of publications themselves — although they did grumble at the changing state of publications and how smaller findings were published more often.
In practice, they more so blamed the human organization problems — essentially administrative issues — that they saw all around them. The growing conference sizes made it much more difficult to keep up with adjacent fields and scientific meetings. Seminars began to cater to narrower and narrower sub-branches of work rather than broad ones.
These were the places that many researchers leveraged to actually keep up to date on new work and problems in their fields as well as others. But, as money began to funnel into their field in the post-War era, there were more and more researchers and logistical decisions had to be made on how to do things like run conferences and decide who sits in what seminars.
The following Richard Feynman excerpt — taken from a 1973 oral history interview, which was one of a series of interviews between Charles Weiner and Feynman — goes into why, in the early 1970s, Feynman felt physics conferences had begun to grow far less useful than they were during the initial interviews for the series — where Feynman had told positive stories about the state of conferences as recently as 1956:
Weiner: How are they [conferences] going from what you’ve seen over the years? Is this the same kind of continuing tradition of the same kinds of people coming together? Because in the early period — we talked about the meeting where you got up and said: “Mr. Block has an idea that I would like to tell you about,” and you talked at the following meeting on that, and these were very exciting things. Has it continued in that same tradition?
Feynman: No, they’ve gotten too big. For example, they have parallel sessions which they never had before. Parallel sessions means that more than one thing is going on at a time, in fact, usually three, sometimes four. And when I went to the meeting in Chicago, I was only there two days before I broke my kneecap, but I had a great deal of trouble making up my mind which of the parallel sessions I was going to miss. Sometimes I’d miss them both, but sometimes there were two things I would be interested in at the same time. These guys who organize this imagine that each guy is a specialist and only interested in one lousy corner of the field. It’s impossible really to go — so it’s just as if you went to half the meeting. Therefore half is not much better than nothing. You might as well stay home and read the reports.
This is no small thing. Feynman, who never religiously kept up with the literature, was one of many who used these conferences as a primary way of keeping up with the changing state of things.
We find a similar account in Warren Weaver’s autobiography.
In Weaver’s book, once again, we hear a 1970-ish account of a researcher who lived through and was active during the golden era of physics complaining about growing conference sizes, not the growing number of publications, making it more difficult to keep up with related scientific areas. Not only were conferences growing in size, but, in response, they separated various disciplines into their own conferences to make conference logistics more manageable.
Many economists tend to believe that it is the sheer size of the literature causing the problem. But both Weaver’s and Feynman’s accounts seem to more directly blame the highly statistically correlated, but fundamentally different, change in conference dynamics and logistics that came with more and more researchers flooding into the community.
Weaver wrote of the early AAAS, which he was once the President of:
This vast organization, with the largest membership of any general scientific society in the world, embraces all fields of pure and applied science. In the earlier days each branch of science conducted intensive sessions at which its own specialized research reports were given, and there was also some mild attempt to organize interdisciplinary sessions of general interest. Then the meetings got so large that they almost collapsed under their own weight. One group after another, first the chemists, then the physicists, the mathematicians, the biologists found it necessary to hold other and separate meetings. Attendance fell and the function of serving as a communication center between the various branches of science became less effective.
At a time when publications had roughly 10x’d, both Feynman and Weaver chose to talk about the masses of people flooding their conferences (and then conferences being held separately) rather than papers flooding their journals.
While the two were not active in the research community throughout the entirety of the decades-long explosion in journal articles — a scientific career is only so long — they were around for enough of the explosion for their accounts to be quite telling. If you take seriously the ability of individuals like Feynman and (especially) Weaver to diagnose issues in their fields — Weaver ‘saw the whole board’ well enough that he was the primary driver in jumpstarting the field of molecular biology as a grant funder — these accounts are surely not evidence to be disregarded.
How fields grow apart matters
Fields that used to be largely integrated can grow apart for a variety of reasons. On one end of the spectrum, fields can grow slowly grow apart. On the other end, they can rather abruptly divorce. As with a real divorce, divorce does not mean that the two fields do not at all interact anymore, but the frequency and amicability of the interactions do change drastically and abruptly.
The nature of how two fields that frequently produced interdisciplinary research come to separate is very relevant to how much faith we should have in the burden of knowledge hypothesis. If the sheer number of publications is the driving force behind the drop in research that combines disciplines, then a strict burden of knowledge hypothesis supporter would probably expect the amount of interdisciplinary research work to drop (more or less) in lockstep with the number of papers in those fields. However, that is often not what we see.
Let’s continue with the case of math and physics in the mid-1900s. These two once-married fields did grow apart, but it had little to do with the size of the literature.
Robert Dijkgraaf — a mathematical physicist, current Dutch Minister of Education, and former Director of the Princeton Institute for Advanced Study — recently published a book chapter in a volume about the late Freeman Dyson. The chapter talks about the ever-exploratory Dyson’s presence at the Institute and several areas of change during his tenure that he decried. One noteworthy change the mathematician-turned-physicist fought against was the divorce of the two fields within the Institute.
Dyson, a dear friend and mentee of Feynman, said this of the growing propensity of mathematicians and physicists to contribute to each other’s field in the 1972 Gibbs Lecture to the American Mathematical Society. The lecture was titled “Missed Opportunities”:
I happen to be a physicist who started life as a mathematician. As a working physicist, I am acutely aware of the fact that the marriage between mathematics and physics, which was so enormously fruitful in past centuries, has recently ended in divorce.
Dyson was the mathematician who proved the equivalence of Feynman diagrams and the operator method of Schwinger and Tomonaga. His style of work, answering physics questions that required the deep toolkit and experience of a solid mathematician, was not uncommon in his early years. One could view the work of von Neumann or Dirac in a similar vein.
Robert Dijkgraff elaborated on the events leading up to the divorce as follows:
As physics became messy and muddy, mathematics turned austere and rigid. After the war, mathematicians started to reconsider the foundations of their discipline and turned inside, driven by a great need for rigor and abstraction. The more intuitive and approachable style of the “old-school” mathematicians like von Neumann and Weyl, who eagerly embraced new developments in physics like general relativity and quantum mechanics, was replaced by the much more austere approach of the next generation. This movement towards axiomatization and generalization was largely driven by the French Bourbaki school, started by a group of young mathematicians in Paris in the 1930s. They had set themselves the task of rebuilding the shabby house of mathematics from its very foundations, under the motto “structures are the weapons of the mathematician.”
This arbitrary shift in taste — surely fueled, in part, by a post-war glut in American funding for research much more basic than before — encouraged young mathematicians to pursue problems in those areas rather than working on physics-related problems. The relationship between mathematicians and theoretical physicists began to change in noticeable ways. Dyson described how this affected his own life at the Institute in an interview with Natalie Walchover:
We had a unified school of mathematics which included natural sciences; it included Einstein; it included Pauli and other physicists. So, the mathematicians and physicists in the first 20 years of the Institute worked together. But at that time when I became a professor it just coincided with the time when Oppenheimer became director and there was a divorce largely occasioned by the fact that Oppenheimer had no use for pure mathematics, and the pure mathematicians had no use for bombs. So, there was a temperamental incompatibility. For one year, after I became a professor, we still had meetings of the whole faculty, but after that they were separate. We had meetings of the physicists and meetings of the mathematicians, no longer speaking to each other. So, that was sort of a local manifestation of the divorce.
Things were changing.
For a while, Dyson was exempt from exclusion on either side — he was a ‘real’ mathematician who simply had success plying his craft in particle physics, just as von Neumann once won fame for plying his mathematical craft in various non-math fields. But, eventually, this new wave of mathematicians did not want him either. He recalled in an interview with his son and science writer, George Dyson:
But I had the advantage, of course, that I was also a mathematician And the mathematicians knew that I had done some useful stuff in pure mathematics. And so, when I appeared here as a professor, I was actually invited to the faculty meetings in mathematics. And for several years [in the mid-1950s] I used to go to the mathematicians’ faculty meetings. And they were quite friendly. They considered me as one of them…So, for the first two years or so I functioned as a mathematician. But at some point, I was, I don’t remember how this happened, but I was dropped, and it was made clear that they didn’t want me at their meetings. So, they regarded me, at first, as being on their side, but then afterwards they found I wasn’t.
In this Dyson description, we see strong hints of academia beginning its march toward the siloed beast we know it as today.
In general, a divorce like this is not symptomatic of a ‘burden of knowledge,’ but, rather, a changing set of incentives and systems taking hold. One could say ‘maybe the fields would have grown apart (at some point) anyway if it weren’t for this systems-related divorce’ just as they could say ‘maybe Weaver and Feynman would have eventually started complaining about the size of the literature as it went from 10x to 30x the original size’ — even though they didn’t complain about it 10x’ing. If one wants to play counterfactual history in that fashion, they can. But we should take the events as they actually happened much more seriously.
With the American boom in post-war basic research funding, obligations for American researchers to have specific, short-term applications in mind for their work became lighter than ever. So, if a field was made up of individuals whose propensity leaned towards mathematical elegance and rigor over real-world applications, they now had more leeway to do that kind of thing. In fact, it might even be encouraged.
This style of thinking can quickly lead to intra-disciplinary work — and the creation of inward-looking sub-branches of science — rather than work that connects fields of separate departments or builds towards concrete applications. American academia was becoming a different world: more people, more funding, more bureaucracy, more silos.
A different world
Gerald Holton, writing at the end of a boom period in several scientific subjects in the mid-1900s, felt that ideas were getting easier to find. He was not the only researcher to think this. It seemed that whenever scientists found a new idea, in line with certain combinatorial theories of innovation, they now had a new hammer to use on existing nails. Alternatively, they could re-combine the idea with other existing ideas to see what happened. Doing this was speculative and prone to more misses than hits, but, to the researchers, the positive expected value of the work was obvious and many were excited to do the work. More importantly, they felt free to do so.
The era recounted in Dyson’s stories of the IAS corresponds with the onset of the modern, increasingly discipline-oriented organization of science. This is an era in which many feel publishing in multiple areas and extreme novelty are disincentivized in various ways due to current journal, grant, and tenure processes.
All of this has happened, coincidentally, as we’ve eased into a world in which it feels like ideas are getting harder to find rather than easier to find. My previous piece, When do ideas get easier to find?, documents Gerald Holton’s mid-1900s work on what seemed to be driving the productivity of early-to-mid-1900s physics. His model of the contemporary ‘physics production function’ placed an extremely high valuation on the importance of incentivizing the workflow of an individual like John von Neumann or the branch-creating inventions of a researcher like I.I. Rabi — whose work many subsequent Nobel prizes depended upon.
Theirs were results worth failing towards.
Holton documented — both anecdotally and with a graph documenting the productivity of research on particle accelerators — that the productivity of fields he was familiar with seemed to be almost entirely driven by the consistent creation of new branches of research. Holton, who was a physicist before he became something of a progress studies researcher, was telling the story of his own field.
As the following graphic shows, exponential growth (logged y-axis) in accelerator energies over several decades was achieved almost entirely by the consistent creation of new technologies and approaches to attack the same problem. The rate of progress for any individual branch of technology usually curtailed quite rapidly after its first 5 years or so, but new branches took its place.
He noted that the creation and extension of these new branches tended to be the domain of the young. Beating a long-tenured professor in an area of knowledge in which they have been building up minute knowledge for several decades is quite difficult. Knowing only 80% as much as the elder statesman doesn’t count for much on older branches of science. But understanding the old ideas, in a nutshell, is plenty when looking to apply the learnings of an old branch to another area of knowledge. When doing that sort of work, enthusiasm and willingness to take some risks count for much more. Most importantly, the young researchers tended to be the most tolerant of this failure-prone and open-ended exploration. They were often excited by it. It was a great way to make a name for yourself!
Holton did not choose this accelerator example because he felt the underlying dynamics driving its growth were any different from those that people believed to be present in the rest of the field. Similar to the choices made in the Bloom paper, it was just the most readily measurable example.
Building on his point, Holton noted that, at the time of writing in around 1962, work by M.M. Kessler had recently found that 50% of the references cited in the Physical Review — the top physics journal at the time — were less than three years old. And only 20% were more than seven years old. Decades on from the paradigm-changing discoveries of relativity and quantum mechanics, physics researchers had still been rapidly leapfrogging each other in the race for human progress, constantly citing young papers and letters. Science was moving so fast that a non-negligible number of citations in the journals were citing personal correspondence and conversations with other physicists as opposed to published papers.
I don’t believe Holton’s theory contradicts the evidence in the Jones and Weinberg paper, either. Even though the authors only examined the quantum revolution by name, there was a second, generally similar burst in theoretical knowledge that their data captured that they did not discuss — the birth of the field of molecular biology. I’m not sure why they omitted this, but it might be that the emergence of molecular biology and the magnitude of its importance is generally paid less attention to than quantum mechanics.
This young branch is one that I covered at length in a previous piece on this Substack. The piece details the dynamics of the burst in branch-creating science in the field of molecular biology between around 1933 and 1953. As the following graph shows, the chemistry Nobel Prize also experienced a resurgence in youth around this time.
The bump would probably look even starker if molecular biology didn’t split its Nobel Prizes between the chemistry and medicine categories.
Looking at the author’s Nobel in Medicine charts, things are less stark. But that should not be surprising. Medicine is a very broad field, handing out Nobel prizes to things like molecular biology discoveries that add to our theoretical understanding of medicine as well as applied findings such as “discoveries concerning heart catheterization and pathological changes in the circulatory system.” So, while the aggregate age trends in medicine don’t exhibit a similar bump (as I show below), the growth in the frequency of theoretical findings responsible for Nobel prizes in this period did experience a noticeable bump. And, as the authors pointed out, in the data theoretical findings were very strongly associated with youth. But, in general, making sense of the mixed bag of research projects that qualify for Nobels in medicine as a single statistical category is maybe not worth looking into too deeply.
Next, we look further into the figures to assess the validity of Holton’s observation that, decades after the start of the quantum revolution, the research being cited in the Physical Review was still extremely young. The larger citation dataset in the appendix of the Jones and Weinberg paper does nothing to make us doubt Holton’s observation. While the smaller, Nobel-prize-only data in the main paper observed shows steady increases in the age of citations, a different trend entirely comes to light in the more robust datasets used in the appendix — which include the 100 most cited papers per year in each field rather than just the Nobel-winning discoveries. In physics and chemistry, it seems that there is more or less a plateau — or extremely marginal decrease — in average citation age from around 1900 to 1970. Then, somewhat abruptly, there begins a significant and steady climb in citation age. One could interpret this, simplistically, as knowledge beginning to progress more slowly.
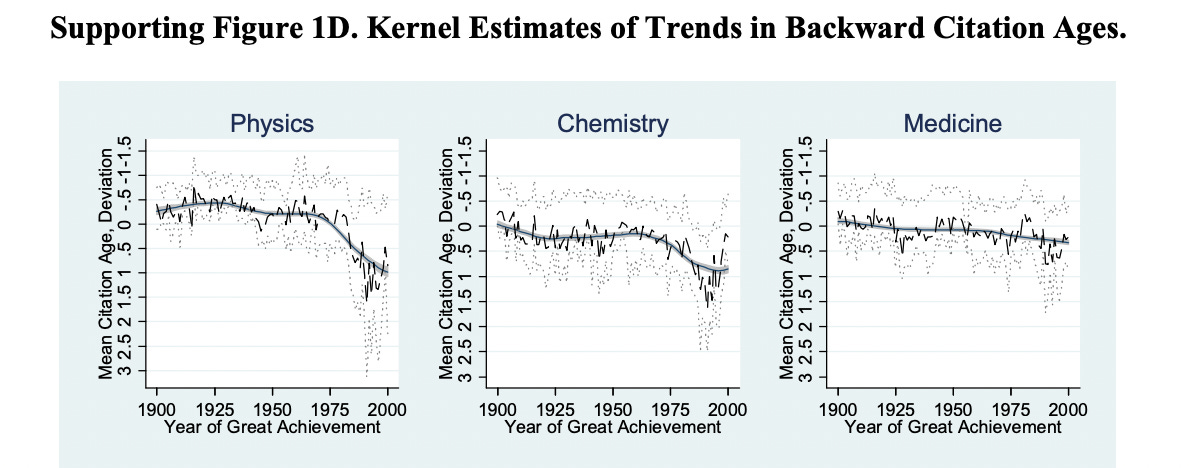
Interestingly, this late-1960s/early-1970s period is also when a lot of the data in papers like Bloom et al’s tends to begin. This is also about the time when Weaver and Feynman’s statements — pointing to a noticeable problem forming in science’s systems — take place. The historical perspective, when examining a question like this, is imperative.
Holton’s model — along with Feynman and Weaver’s statements — came right at the end of a bit of a golden era. Holton’s model describes a different world, but one that is very relevant to the question of how to re-ignite scientific productivity.
Reflecting on how there were a growing number of problem areas where headway could be made by individuals from as many as five fields, Holton asserted that:
It is becoming more and more evident that departmental barriers are going to be difficult to defend.
He believed that we might see the end of departmental barriers and a system that evolved to incentivize all-important, branch-creating science. Young branches were where the most productive science was done. Young branches are where the burden of knowledge isn’t so burdensome. He believed we would build institutions and systems focused on creating new branches above all else because that’s what was driving our productivity.
We built the exact opposite.
What ‘Poetry and Ambition’ can teach us
As you know, we cannot re-run recent scientific history, changing individual parameters as we wish. What if institutions and incentives hadn’t changed 50+ years ago? What if we could set the ‘burden of knowledge coefficient’ to zero and re-run the simulation with the same institutional changes? This inability is one that haunts social scientists every day.
But, luckily, we do have a case study available to us that provides a lot of perspective — and lends a lot of credibility to the human systems hypothesis. There is a non-STEM field where institutions and incentives similar to those introduced to American STEM research in the late-1900s were introduced. The field, to most people’s eyes, is subject to rather negligible burden of knowledge issues. And when similar institutions were introduced into the field, similar changes occurred.
It is an imperfect analogy, but one that comes close to setting the burden of knowledge coefficient to zero and re-running the simulation with similar institutional changes to observe how much of the slowdown persists.
The field: poetry.
Many within the field of poetry and creative writing in general, apparently, believe they are living through an extreme slowdown in work of the highest quality as well. This is something I was unaware of until recently when an unusually broad-ranging mathematician friend of mine, Chen Lu, began telling me about it and shared the piece on which this section is based. The piece is called Poetry and Ambition. It is a long, part essay/part poem published by Donald Hall who was a practicing poet from 1950 through the early-200s.
In Poetry and Ambition, Hall highlights the changing state of the field over his career in terms of goals, outcomes, incentives, and overall ambition. In many of the sections, if one replaces words like ‘writer’ and ‘poem’ with ‘researcher’ and ‘finding’, the excerpt sounds eerily similar to complaints from those in the progress community railing against science’s stagnation.
For example, Hall writes the following on the changing ambitions of the poet:
5. True ambition in a poet seeks fame in the old sense, to make words that live forever. If even to entertain such ambition reveals monstrous egotism, let me argue that the common alternative is petty egotism that spends itself in small competitiveness, that measures its success by quantity of publication, by blurbs on jackets, by small achievement: to be the best poet in the workshop, to be published by Knopf, to win the Pulitzer or the Nobel. . . . The grander goal is to be as good as Dante.
Let me hypothesize the developmental stages of the poet.
At twelve, say, the American poet-to-be is afflicted with generalized ambition. (Robert Frost wanted to be a baseball pitcher and a United States senator; Oliver Wendell Holmes said that nothing was so commonplace as the desire to appear remarkable; the desire may be common but it is at least essential.) At sixteen the poet reads [Walt] Whitman and Homer and wants to be immortal. Alas, at twenty-four the same poet wants to be in The New Yorker. . . .
To be clear, Hall is not some rogue in his beliefs. Mark McGurl wrote the following in his book, The Program Era, on postwar fiction and its effects on the field of creative writing:
While the existence of degree-granting entities like the Iowa Writers’ Workshop was the result, in part, of a new hospitality to self-expressive creativity on the part of the progressive-minded universities willing to expand the boundaries of what could count as legitimate academic work, the founders and promoters of these programs more than met the institution halfway, rationalizing their presence in a scholarly environment by asserting their own disciplinary rigor.
Halls words simply attempt to (eloquently) describe a wider trend.
Hall goes on to refer to the type of poem that the exploding poetry and MFA programs have geared themselves to train poets to produce as the ‘McPoem.’ “To produce the McPoem, institutions must enforce patterns, institutions within institutions.” These misguided forms of quality controls, in Hall’s eyes, were how most large American organizations had adapted themselves to meet the needs of larger and larger audiences who wanted to buy what they were selling. Similarly, this is how MFA programs had structured themselves to meet the increasing need of young people seeking out the degree programs. To him, the approach was far more suited to mass-market goods than his craft.
Hall continues, diving into what the work of the ‘poetic heroes of the American present’ often looked like:
When Robert Lowell was young, he wrote slowly and painfully and very well. On his wonderful Library of Congress LP, before he recites his early poem about “Falling Asleep over the Aeneid,” he tells how the poem began when he tried translating Virgil but produced only eighty lines in six months, which he found disheartening. Five years elapsed between his Pulitzer book Lord Weary’s Castle, which was the announcement of his genius, and its underrated successor The Mills of the Kavanaughs. Then, there were eight more years before the abrupt innovation of Life Studies. For the Union Dead was spotty, Near the Ocean spottier, and then the rot set in.
Now, no man should be hanged for losing his gift, most especially a man who suffered as Lowell did. But one can, I think, feel annoyed when quality plunges as quantity multiplies: Lowell published six bad books of poems in those disastrous last eight years of his life.
He continues:
9. Horace, when he wrote the Ars Poetica, recommended that poets keep their poems home for ten years; don’t let them go, don’t publish them until you have kept them around for ten years: by that time, they ought to stop moving on you; by that time, you ought to have them right. Sensible advice, I think — but difficult to follow. When [Alexander] Pope wrote “An Essay on Criticism” seventeen hundred years after Horace, he cut the waiting time in half, suggesting that poets keep their poems for five years before publication. Henry Adams said something about acceleration, mounting his complaint in 1912; some would say that acceleration has accelerated in the seventy years since. By this time, I would be grateful—and published poetry would be better—if people kept their poems home for eighteen months.
Poems have become as instant as coffee or onion soup mix. One of our eminent critics compared Lowell’s last book to the work of Horace, although some of its poems were dated the year of publication.
…
If Robert Lowell, John Berryman, and Robert Penn Warren publish without allowing for revision or self-criticism, how can we expect a twenty-four-year-old in Manhattan to wait five years—or eighteen months? With these famous men as models, how should we blame the young poet who boasts in a brochure of over four hundred poems published in the last five years? Or the publisher, advertising a book, who brags that his poet has published twelve books in ten years? Or the workshop teacher who meets a colleague on a crosswalk and buffs the backs of his fingernails against his tweed as he proclaims that, over the last two years, he has averaged “placing” two poems a week?
Hall then goes on to describe the MFA and how it has specifically, in his eyes, tainted the process of great poetry. Looking at the passage, one could imagine an eerily similar statement coming from a scientist who practiced from the mid into the late 1900s, talking about how the research process had become much more about detailed methods and learning to conduct a research pipeline slightly more rigorously and less about taking proper time and intellectual effort to do true exploration to find properly new ideas. Hall continues, furiously:
10. Abolish the MFA! What a ringing slogan for a new Cato: Iowa delenda est! [Iowa must be destroyed!] (Iowa possesses the most prominent MFA program.)
The workshop schools us to produce the McPoem, which is “a mold in plaster, / Made with no loss of time,” with no waste of effort, with no strenuous questioning as to merit. If we attend a workshop we must bring something to class or we do not contribute. What kind of workshop could Horace have contributed to, if he kept his poems to himself for ten years? No, we will not admit Horace and Pope to our workshops, for they will just sit there, holding back their own work, claiming it is not ready, acting superior, a bunch of elitists. . . .
When we use a metaphor, it is useful to make inquiries of it. I have already compared the workshop to a fast-food franchise, to a Ford assembly line. […] Or should we compare Creative Writing 401 to a sweatshop where women sew shirts at an illegally low wage? Probably the metaphor refers to none of the above, because the workshop is rarely a place for starting and finishing poems; it is a place for repairing them. The poetry workshop resembles a garage to which we bring incomplete or malfunctioning homemade machines for diagnosis and repair. Here is the homemade airplane for which the crazed inventor forgot to provide wings; here is the internal combustion engine all finished except that it lacks a carburetor; here is the rowboat without oarlocks, the ladder without rungs, the motorcycle without wheels. We advance our nonfunctional machine into a circle of other apprentice inventors and one or two senior Edisons. “Very good,” they say; “it almost flies. . . . How about, uh . . . how about wings?” Or, “Let me just show you how to build a carburetor. . . .”
Whatever we bring to this place, we bring it too soon. The weekly meetings of the workshop serve the haste of our culture. When we bring a new poem to the workshop, anxious for praise, others’ voices enter the poem’s metabolism before it is mature, distorting its possible growth and change.
He later moves on to examine the ill effects of the overt bureaucratization of the poetry profession — where, increasingly often, the university’s creative writing department or adjacent grant funders provided the best chance for poets to earn a steady income practicing some version of their craft. The effects could easily be seen. One only needed look at the industry’s newsletters:
14. A product of the creative writing industry is the writerly newsletter which concerns itself with publications, grants, and jobs—and with nothing serious. If poets meeting each other in 1941 discussed how much they were paid a line, now they trade information about grants; left wing and right united; to be Establishment is to have received a National Endowment for the Arts grant; to be anti-Establishment is to denounce the N.E.A. as a conspiracy.
…
Associated Writing Programs publishes A.W.P. Newsletter, which includes one article each issue—often a talk addressed to an A.W.P. meeting—and adds helpful business aids: The December 1982, issue includes advice on “The ‘Well Written’ Letter of Application,” lists of magazines requesting material (“The editors state they are looking for ‘straightforward but not inartistic work’”), lists of grants and awards (“The annual HARRY SMITH BOOK AWARD is given by COSMEP to…”), and notices of A.W.P. competitions and conventions. . . .
Really, these newsletters provide illusion; for jobs and grants go to the eminent people. As we all know, eminence is arithmetical: it derives from the number of units published times the prestige of the places of publication. People hiring or granting do not judge quality—it’s so subjective!—but anyone can multiply units by the prestige index and come off with the product. Eminence also brings readings. Can we go uncorrupted by such knowledge? I am asked to introduce a young poet’s volume; the publisher will pay the going rate; but I did not know that there was a going rate. . . . Even blurbs on jackets are commodities. They are exchanged for pamphlets, for readings; reciprocal blurbs are only the most obvious exchanges. . . .
I may need to add ‘Donald Hall’ to my list of ‘people who did progress studies before progress studies existed’…
Academics and the system they operated within used to understand that they were in a hit-making game. John Nash, with an h-index of 7, was employed by the profession for decades because they felt he, at any point, had the potential to produce a massive hit. Richard Feynman left new discoveries in his desk constantly. He felt they wouldn’t change much in the field, so they weren’t worth the hassle of publishing. He had more ambition than that. When he did publish interesting and ambitious papers, journals would not reject them because pieces of them were shaky. This Substack covered a case of Feynman publishing a finding, that turned out to be right, in spite of Bohr and Dirac openly saying beforehand they thought it was completely wrong. It was an amicable disagreement — most were. The journals were the best place to debate that sort of thing, so it was published!
Hall’s final paragraph, in a way, touches on all of this:
16. There is no audit we can perform on ourselves, to assure that we work with proper ambition. Obviously, it helps to be careful; to revise, to take time, to put the poem away; to pursue distance in the hope of objective measure. We know that the poem, to satisfy ambition’s goals, must not express mere personal feeling or opinion—as the moment’s McPoem does. It must by its language make art’s new object. We must try to hold ourselves to the mark; we must not write to publish or to prevail. Repeated scrutiny is the only method general enough for recommending. . . .
And of course repeated scrutiny is not foolproof; and we will fool ourselves. Nor can the hours we work provide an index of ambition or seriousness. Although Henry Moore laughs at artists who work only an hour or two a day, he acknowledges that sculptors can carve sixteen hours at a stretch for years on end—tap-tap-tap on stone—and remain lazy. We can revise our poems five hundred times; we can lock poems in their rooms for ten years—and remain modest in our endeavor. On the other hand, anyone casting a glance over biography or literary history must acknowledge: Some great poems have come without noticeable labor.
But, as I speak, I confuse realms. Ambition is not a quality of the poem but of the poet. Failure and achievement belong to the poet, and if our goal remains unattainable, then failure must be standard. To pursue the unattainable for eighty-five years, like Henry Moore, may imply a certain temperament. […] If there is no method of work that we can rely on, maybe at least we can encourage in ourselves a temperament that is not easily satisfied. Sometime when we are discouraged with our own work, we may notice that even the great poems, the sources and the standards, seem inadequate: “Ode to a Nightingale” feels too limited in scope, “Out of the Cradle Endlessly Rocking” too sloppy, “To His Coy Mistress” too neat, and “Among Schoolchildren” padded. . . .
Maybe ambition is appropriately unattainable when we acknowledge: No poem is so great as we demand that poetry be.
Ambition is not something to be metered and rewarded accordingly — it’s not possible. But everything possible should be done to, at the very least, not disincentivize it.
Poetry is only so similar to science. But it does seem that — even though in the American tradition writers and scientists do not co-habit the same areas of the intelligentsia as they do in Russia — many in both groups that lived through similar systems changes come together in the belief that the new institutions and incentives tainted their fields.
It’s not so silly to think that what happened to the field of poetry could inform how we think about counterfactual scientific history. As much as there are great scientists who learn by reading, the number of stories of great science as a predominantly learning-by-doing exercise abound. It’s not so silly to give serious consideration to the case of writers and the state of their field. Writers, after all, also spend substantial amounts of time formulating new ideas, perusing the works of peers, and attempting to deploy both new methods and ideas into their own work.
Surely, the burden of knowledge is more burdensome in science than in writing. But, it should not be forgotten, that many of the great scientists I’ve covered on this Substack didn’t place nearly as high a priority on ‘keeping up with the literature’ as modern researchers.
Edison spent time on it, but he spent far more time at the lab bench learning things for himself. He both kept up with and was extremely skeptical of the literature.
And if the reader feels that Edison’s era of electrical science was somehow primitive and is not representative, Willis Whitney — a former academic — eventually instituted a rule at the GE Research Lab where you’d get in trouble for going to the library too frequently. He learned, through early failures in relying too heavily on the literature, that it had limited effectiveness in solving problems — compared to experimentation and working with colleagues.
Not to belabor the point, but Feynman was also notorious for not exactly keeping up with the literature. He kept up to some extent, but often worked things out for himself, later checking the literature to see if he was the first one to have done that. He felt that was the best way — both to understand things and also to practice the process of figuring things out.
A different world — with different systems — yielded a different kind of researcher.
If true, how does the human systems hypothesis change things?
To me, the idea that the slowdown in scientific ideas might be driven far more by changes in human systems and incentives than some force of nature related to growing ‘idea space’ is great news. While solutions can likely be found to mitigate issues associated with the more standard burden of knowledge hypothesis, we’re still working against constraints of nature. In the world where it’s a human systems issue, we’re mostly working against people!
Working against people isn’t easy, but it’s doable. We’re already making great first steps. Progress studies funders have been very forward-thinking in funding new, experimental science orgs such as Arc Institute, Arcadia, and Convergent Research (with more to come) that provide invaluable learning opportunities on a small scale. Any learnings that prove successful on that small scale can grow into medium-term efforts — possibly even whole research institutes — which can scale, continue to experiment, and (hopefully) find even more success. In the longer run, the federal government — an effective copycat of ideas that have been de-risked and aren’t too politicized — could fold these learnings into their existing NIH and NSF policies. Or, as is often the case in government scientific history, they may start a new department to take advantage of the new learnings.
The pressing question then is: what are the best things these new science orgs can do?
The most general and boring answer is twofold:
Make sure you’re trying something truly different from existing efforts. We need novelty.
Document as much as possible about your novel attempt so we can learn from it!
My more prescriptive (and interesting) answer is also twofold:
Do more truly applied research! This was largely America’s biggest comparative advantage in research throughout the early-1900s. We found ways to let this process drive great basic research and vice-versa. I’ve written up detailed accounts of many different ways to do this that proved successful on this Substack:
How did places like Bell Labs know how to ask the right questions?
Irving Langmuir, the General Electric Research Laboratory, and when applications lead to theory
A Progress Studies History of Early MIT— Part 2: An Industrial Research Powerhouse
Tales of Edison's Lab & Thomas Edison, Technical Entrepreneur
If you’re doing basic research, focus on creating new scientific branches at the expense of all other things! It’s a right-tailed game, and it’s extremely worth it. As the pieces listed above detail, these new branches can often result from applied research projects if managed the right way — with researchers given certain problems and certain freedoms. The following pieces document processes that yielded branch-creation in a more (traditional) basic research setting:
To conclude, I implore the reader to remember something that Weaver, Feynman, Dyson, and Holton would agree upon: the way science is done is indelibly impacted by the way scientists are organized and incentivized. If you spoil their excitement and ambition, the whole enterprise becomes entirely different. The magnitude of change that can result should not be underestimated.
Thanks for reading:)
In the near future, I would love to document — one by one — the historical details of why fields that used to work together closely grew apart. That kind of brute force project would go a long way in further addressing the question in today’s piece. If you’d like to help on that project, please reach out — it will take more people than just me!
Also, Chen Lu — the mathematician I mentioned — is finishing his Ph.D. in applied math at MIT and is looking for a job. Something like ML roles where he can use his math and coding toolkit would be ideal. You can check out his LinkedIn here and some of his publications here. If you’d like an intro, DM me on Twitter!
Appendix
When showing this paper around, one economist of innovation asked how I felt about Agarwal et al.’s paper on the growing size of publishing teams in mathematics in the aftermath of the Iron Curtain falling. I thought this was a very fair point and worth including, but one that would break up the flow of the main piece as it is a bit of an aside.
Before speaking briefly on the Agarwal paper, I should first start by explaining the previous and more well-known Borjas and Doran paper whose data Agarwal et al. used in their analysis. Borjas and Doran put together a dataset on the publications, citations, university affiliations, and more of both Soviet mathematicians as well as American mathematicians before and after the Iron Curtain falling. They pay special attention to the different effects the shock had on American mathematicians who were publishing in fields that the Soviet’s were particularly strong in vs. those where they were comparatively weak.
As the authors note, in spite of the fact that there were around 2.4x as many American mathematicians and Americans published 3x as many papers overall, there were areas in which the Soviets were far stronger, publishing 1.4x as many papers as Americans and having the undeniable world leaders in the space. There were also areas where the Soviet Union was essentially a non-factor, publishing around .05x as much as Americans. The following graphic gives you an idea of just how wide the difference was across fields — the bar measures the ratio of Soviet papers to American papers in a topic area.
Paying close attention to the labor market effects in the aftermath of the shock, the authors find (among other things):
The overall number of papers written by professors at American universities was more or less unchanged after the Iron Curtain fell.
The number of papers written per American mathematician and by American mathematicians overall went down, but this was counteracted by the effective increase in total Soviet-descendant professors publishing.
American professors who published in the weakest Soviet disciplines were more or less unaffected, whereas those who published in Soviet areas of strength ended up publishing less, received fewer citations, were more likely to end up unemployed or at a worse university, etc.
However, if an American professor in an area of Soviet strength co-authored with a Soviet professor, it seems this was correlated with being unaffected.
Around 1/8th of new professorships were being given to Soviet mathematicians immediately after the Iron Curtain fell, and these immigrants were particularly strong.
In general, I believe the Borjas and Doran observations in all of these areas are quite strong. As a dataset informing the labor market effects of the Soviet influence in American math academia from around 1975-2010 — which is what the paper claims to be — the methods and takeaways seem interesting and robust.
In the author’s own words, they summarize their results as follows:
Soviet mathematics developed in an insular fashion and along different specializations than American mathematics After the collapse of the Soviet Union, over 1,000 Soviet mathematicians (nearly a tenth of the pre-existing workforce) migrated to other countries, with about 30 percent settling in the United States. As a result, some fields in the American mathematics community experienced a flood of new mathematicians, theorems, and ideas, while other fields received few Soviet mathematicians and gained few potential insights.
Our empirical analysis unambiguously documents that the typical American mathematician whose research agenda most overlapped with that of the Soviets suffered a reduction in productivity after the collapse of the Soviet Union. Based solely on the pre-1992 age-output profile of American mathematicians, we find that the actual post-1992 output of mathematicians whose work most overlapped with that of the Soviets and hence could have benefited more from the influx of Soviet ideas is far below what would have been expected. The data also reveal that these American mathematicians became much more likely to switch institutions; that the switch entailed a move to a lower quality institution; that many of these American mathematicians ceased publishing relatively early in their career; and that they became much less likely to publish a “home run” after the arrival of the Soviet émigrés. Although total output declined for the pre-existing group of American mathematicians, the gap was “filled in” by the contribution of Soviet émigrés
I think that is a great paper and I value the results a lot.
Agarwal et al., four years later, use mostly the same data and attempt to tell a burden of knowledge hypothesis story with it. I don’t think it would be an unfair interpretation to say that their work surely approximates — to some extent — something of an upper-bound on the ‘burden of knowledge coefficient,’ but I believe it would be a stretch to say it establishes any kind of well-identified lower-bound. I’ll begin to tell you why in the next paragraph. But, before I do, it is probably worth pointing out that — in spite of Ben Jone’s paper on the burden of knowledge having been published several years before the Borjas and Doran paper — Borjas and Doran did not choose to make claims about their data as demonstrating proof of the burden of knowledge in their paper.
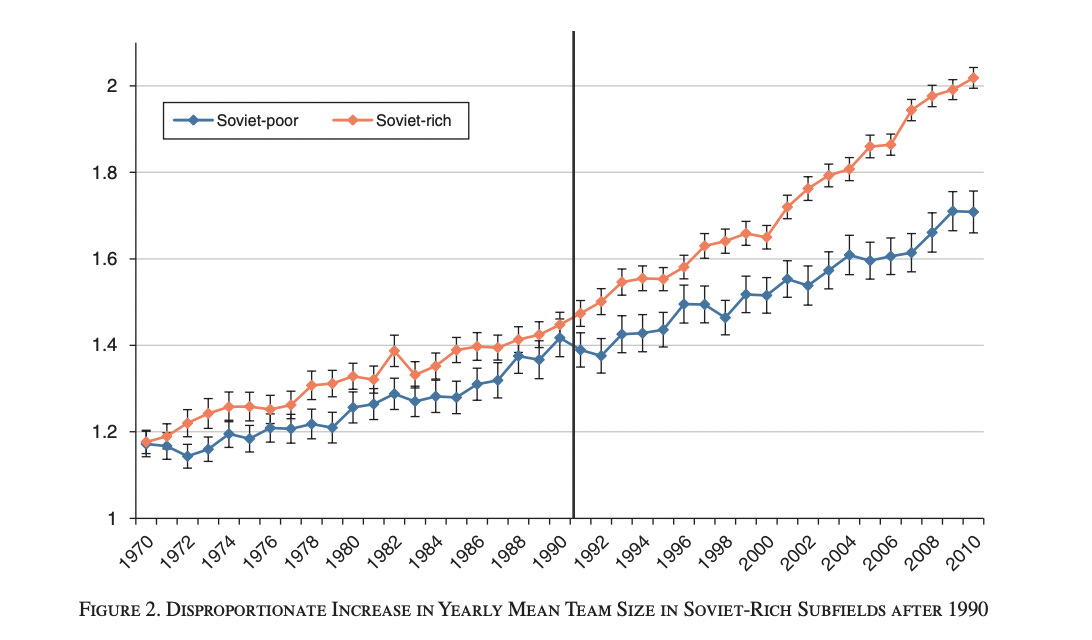
Agarwal et al., however, do attempt to make this claim using largely the same data. I don’t think it’s unreasonable for the journal to have published the paper, but I do think the results are not nearly as robust as Borjas and Doran’s and should be used with caution. Agarwal et al. attempt to exploit the difference in team size trends between the three sub-fields in which the Soviets were strongest and the three sub-fields in which the Soviets were the weakest. The trend they’re looking at is visualized below — with the orange line representing American team size in Soviet-rich areas and the blue the team size of areas of Soviet weakness.
As is common, the starting point of the data is in 1970. From 1970 to 1991, there is a slow and steady rise in both lines, then — and around the fall of the Iron Curtain — the author count in Soviet-rich sub-fields begins to climb at a higher rate. The authors wrote, “For the treated subfields (Soviet-rich), the mean team size for the 20-year period before 1990 was 1.34 compared to 1.78 for the 20-year period after. By comparison, for the control subfields (Soviet-poor), the mean team size was 1.26 before compared to 1.55 after.” That increase in .29 authors per paper in the ‘control’ group vs. .44 in the ‘treatment’ group is observational and not to be disputed. In relation to how this affects the human systems hypothesis, the grains of salt I take their solutions with — as they do/don’t apply to the hypothesis — have to do with 1) what the authors could not control for that also change around this period and 2) the time period of American academia in which the shock occurred.
The first grain of salt I take this chart in with is that all of the changes resulting from this shock are happening in a post-1970 American system which I’ve never disputed has certain norms and systems for accounting for new ideas that would make things like team size grow. That is my biggest issue, but it is also unsurprising, I’m sure.
The second grain of salt I take the results in with is that the effects of a knowledge shock that result from an entire country’s ideas — that have been built of over decades — reaching the world are probably not the same as when individuals or small teams produce an idea. One major difference being: if it’s just one researcher’s big and new idea, there is only one of them to go around. In the Iron Curtain case, there were 12,000+ other researchers who had been familiar with many of the ideas for a while. 1,000+ of the most talented ones abruptly left to research abroad in other country’s. When combined with the first grain of salt, this could impact the trends we see in the data in a way that is not representative of the standard case of idea creation.
The third grain of salt I take the paper with is that it does not control for the labor market influx of Soviet researchers to the US.1 And the influx was non-negligible. In fact, the labor market shock itself was what Borjas and Doran exploited in their paper. Borjas and Doran noted that around 1/8th of new professorships in the post-Iron Curtain falling years were going to Soviets — and quite inordinately talented Soviets. In an attempt to show that their results were robust to this, Agarwal et al. show a chart of Japan because Japan had almost no Soviet mathematics immigrants. They ran other regressions as well, but, first, I’ll address the Japan chart — the only other country’s chart they chose to show.2
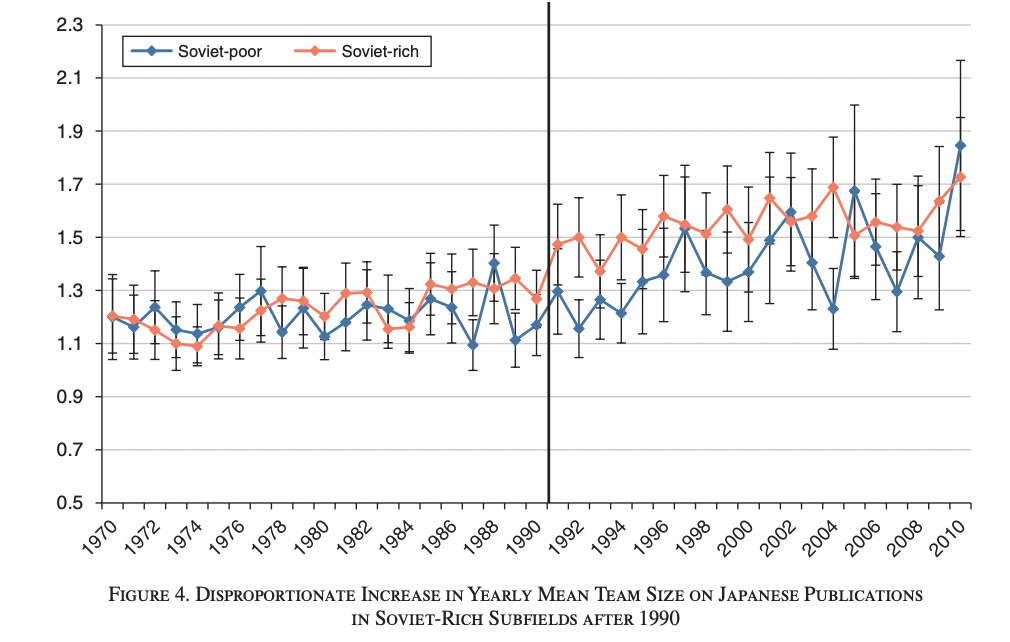
Looking at the chart, I found it strange that the Soviet-poor fields had such steady team size numbers pre-fall of the Iron Curtain but then began a noticeable and steady climb after the Iron Curtain fell. Agarwal et al. did not mention this which I found strange, because whatever happened there is significantly larger than the effect noted by the distance between the orange and blue lines. This distance between the two lines is what the authors’ regressions concern themselves with. I asked an economics of innovation-related researcher who works with the Japanese government if anything happened in the early 1990s as well. He laughed and said that the years around 1995 marked extremely important changes. This period saw substantial increases in government input, funding, and planning for many types of scientific grants.
I asked some questions about how these worked, and it seems like the new policies were often very NIH-like — large government employee oversight, sizable panels, proposal processes, etc. So, I don’t personally take that Japan chart very seriously — unless you are very compelled by the first three pairs of dots post-Iron Curtain falling, in which they noisily grow apart and back together again before the onset of the government changes. If I did take the chart seriously, accounting for the change in human systems, it very well could tell a story that points the finger more towards the human systems hypothesis as driving the overall changes more so than the burden of knowledge hypothesis.
The regressions the authors ran on other countries — which they did not visualize — are essentially tracking the same thing — the statistical significance of the growth in the gap between those two lines before and after the iron curtain fell. (Half of these countries’ regression coefficients did not come out as significant at the 95% confidence interval.) As with the Japanese chart, the paper does not seem to pay attention to the fact that there could be much more significant changes happening elsewhere in the system that the methods (and authors) are unaware of and don’t account for. I don’t blame them because it is extremely burdensome — on the order of months — to figure out exactly what happened in even a handful of countries' scientific grant-funding ecosystems over that timeline. But, what matters for our interpretation is that they didn’t. Here is a 1995 Nature article titled Japan opens a new era in university funding very publicly exploring some of these changes.
(Also, see Figure 2-10 at this link, Trends in Budget for Grants-in-Aid for Scientific Research, showing related funding changes impacting trends as early as 1991.)
Speaking frankly, anything could have been happening around 1991 in any number of those countries that the authors do not know about. In the best case, the method only identifies the existence of a burden of knowledge and does nothing to identify the burden of knowledge effects as anything more than existing and being statistically significant — saying nothing about its presence as a primary driver of stagnation. And, once again, that is if you buy into the premise of their natural experiment as a natural experiment at all.
I read this paper as doing an okay job (at best) of isolating the presence of a burden of knowledge-type effect in the US ecosystem conditional on the shock being introduced to the post-1970 US ecosystem. I believe the coefficient estimates themselves are very likely overestimated. It is highly likely that they capture the effects of things that the authors did not/could not control for, such as: the new system itself interacted with the math field type, the full effects of new Soviet colleagues on their American colleagues, and the effects of the “knowledge” coming from 12,000 people all at once rather than a handful.
Natural experiment papers can only be as strong as the natural experiment itself. And there’s just a lot of moving parts here. Throughout this piece, I’ve used many papers whose results maybe get over-interpreted by others, but that I think are great and well-done papers that are very thorough. This paper — unlike the Borjas and Doran paper written using the same event as a shock — is one that I think should be used more carefully.
The authors attempt to run one of their regressions dropping all Soviet last named papers and said their regressions were still robust. But they acknowledged that this was not enough to control for all of the effects Soviets could have on their sub-field by having been incorporated into an American researchers hallway and social circle. The authors acknowledged the Japan evidence as their primary reasoning for their findings being robust to this labor market confounder, saying, “Secondly, and perhaps most importantly, we show the same pattern persists in Japan, a country that experienced very little immigration of the Soviet mathematicians.”
Much of the observational work in the Borjas and Doran paper exemplifies why merely dropping the Soviet-named publications only scratches the surface on the effects the Soviet emigré mathematicians could have on a mathematician and the department/field as a whole. That is why this Japan analysis was so vital to do.
For some reason, Figure 6 in the paper shows China as insignificant at the 95% confidence interval, but their table has three stars indicating it significant at the 99% interval. But, looking at the table, the standard error and coefficient make me believe that China’s results in Figure 6 are more likely to be insignificant at the 95% interval rather than significant at the 99% interval. But I wanted to note this (what I think might be a) discrepancy.










Hall did not notice (deliberately or otherwise) the huge and flourishing field of Black poetry that is now widely recognized. He was pretty siloed. But the point stands: innovation comes often from unexpected (to some, to others expected and long delayed) quarters.
"Surely, the burden of knowledge is more burdensome in science than in writing." Quite the opposite. The burden of Dante, Milton, Shakespeare etc already existing is far more problematic to poets than the existing scientific knowledge. Harold Bloom and The Anxiety of Influence is a good place to start for that.